From A-levels to pensions, algorithms make easy targets – but they aren’t to blame
Jonathan Everett; Guardian Tue 17 Aug 2021 09.00 BST
Poor policy outcomes are not the responsibility of ‘mutant maths’, but of choices made by people in power
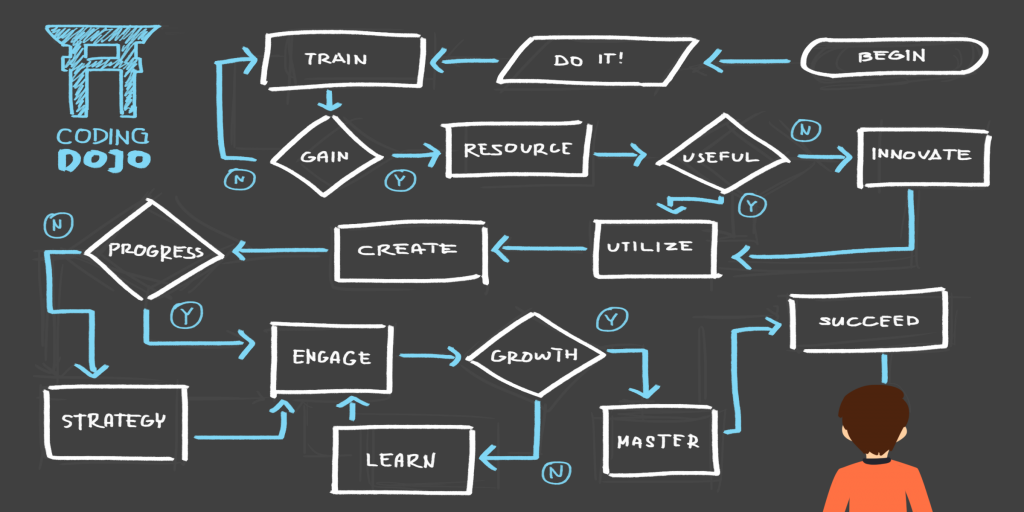
‘The government’s occasionally misleading use of modelling – such as when it mispresented Covid projections while making the case for a second lockdown in October last year – has not built confidence.’ Boris Johnson announces the second lockdown for England, 31 October 2020. Photograph: WPA/Getty Images
A year ago, when the prime minister blamed a “mutant algorithm” for A-level students receiving lower than their predicted grades, a new phrase entered political discourse. Since then, the government’s proposed housing algorithm has been labelled “mutant” by the Conservative MP Philip Hollobone; recently even the pensions triple lock was referred to as a “mutant formula” by the GB News journalist Tom Harwood.
It’s worth thinking about why this wording has spread. The implication of calling an algorithm “mutant” is that technology has got out of hand and that a useful mathematical system has produced perverse outcomes when applied in the real world. But this obscures the reality, which is that people in power choose when to use algorithms, set their parameters, and oversee their commissioning process. Those developing algorithms repeatedly check they are doing what ministers want them to do. When algorithms are spoken of as “mutant” it obscures this reality, framing algorithms as outside forces that act upon us, rather than tools that can help us understand the world and make decisions.
These algorithms aren’t “mutant” in any meaningful sense – their outcomes are the inevitable consequence of decisions made during their design. As soon as you make the decision to place a small limit on grade inflation and award grades to individuals based on how their schools have ranked them, it follows that some pupils will have their grades unfairly lowered. Likewise, the consequence of the housing algorithm – unpopular housebuilding in Conservative seats – was so foreseeable that backbench disquiet prevented it seeing the light of day. The triple lock is precisely intended to be a commitment to keep the state pension rising at a minimum of 2.5%, and potentially more. This may seem like a lot when a government is otherwise looking for places to make cuts, but it is not a surprise – it is what the triple lock is.
We shouldn’t blame mutant maths for poor policy outcomes. The responsibility lies with the people who commission and deploy the algorithms. It is tempting to wonder whether something else might be going on here. Whether, rather than these being genuine critiques of algorithms as a malign force, these interventions are part of the long tradition of indirect criticism of rulers: it is not the king who is responsible, but his evil adviser. It is costly for some of the people who are using this language – a backbench MP and a journalist close to the governing party – to criticise the government directly. Perhaps mutant maths is simply a neat way of criticising government policy without appearing disloyal to the government itself.
This move is even quite explicit on some occasions, such as when the Conservative MP Neil O’Brien described the government’s housing planning formula as “the next algorithm disaster”. After detailed discussion of what the algorithm does, O’Brien, a very loyal Conservative, is careful to say that he’s “not sure the … algorithm is even doing what ministers wanted it to”.
Viewed this way, it’s clear why such language is attractive to people who are generally supportive of the government. But it still doesn’t explain why the phrase “mutant algorithm” has such widespread appeal. Part of its power reflects a wider societal scepticism about the use of statistics, algorithms and modelling in policymaking. This is perhaps why, when discussing the process for awarding grades this year, ministers and government websites all proudly championed the lack of an algorithm as a positive virtue.
Some of this scepticism is understandable. The attempt to use an algorithm to award grades was poorly considered and handled. When the unfairness of the government’s approach became clear, the algorithm was an easy target for blame. But this approach has clearly dented wider confidence in the use of algorithms in general.
The pandemic has also had a mixed impact on how people view maths and modelling in policymaking. Statistics and data have very visibly helped to improve the public’s understanding of Covid-19 and have improved decision-making. But the government’s occasionally misleading use of modelling – such as when it mispresented Covid projections while making the case for a second lockdown in October last year – has not built confidence.
Statistics provide a powerful set of tools that have the potential to dramatically improve government decision-making, both through algorithms and data-driven forecasting. We have seen this potential put to use during the pandemic; data has informed the decision to enforce lockdowns, convinced political leaders that lockdowns are necessary, and shown the link between Covid-19 case numbers and hospitalisations.
Using statistics to inform policy in this way relies on public confidence. When this starts to unravel, it is very difficult to restore. Statisticians have a role to play here by explaining the limits and uncertainties inherent to algorithms and models. And across government more statisticians are assuming leadership positions and helping to shape the political agenda. But this cannot be the sole job of statisticians: we need ministers and other politicians to treat algorithms as products of human decisions rather than easy sources of blame when things go wrong.
So, when algorithms are used and the outcome is undesirable, let’s be careful to place the blame where it belongs: with the king and not the adviser.
Jonathan Everett is head of policy at the Royal Statistical Society




